#04 Plánovanie dráhy robota

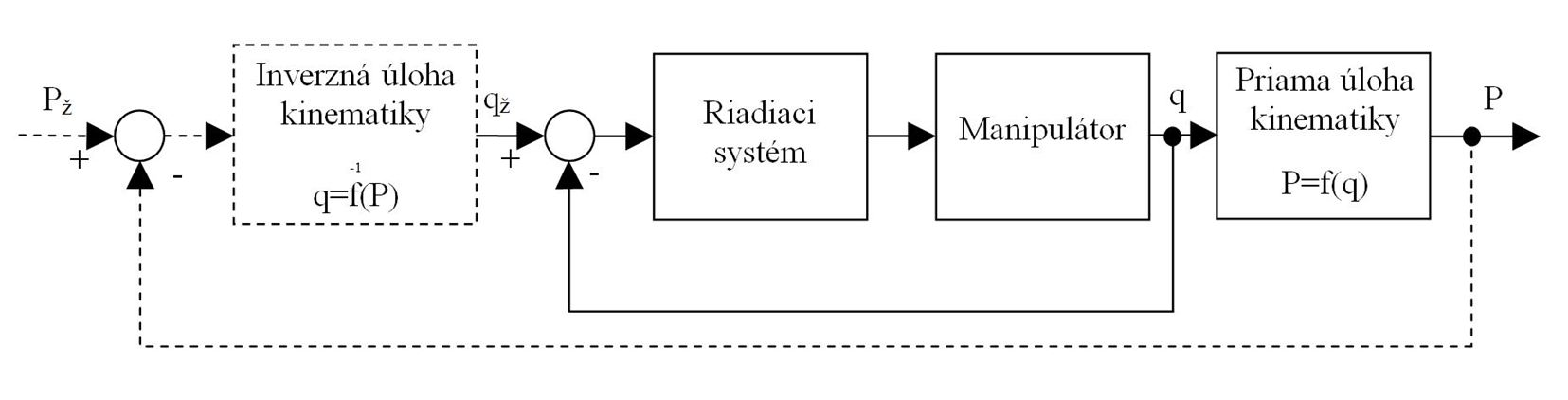
Ku vysvetleniu spôsobu riadenia robota si uvedieme niekoľko potrebných poznatkov ohľadom priamej úlohy kinematiky a inverznej úlohy kinematiky. Znalosť kĺbových súradníc nám umožňuje celkom jednoznačne určiť hodnoty súradníc koncového člena manipulátora v kartézskom priestore. Ak si označíme vektor kĺbových súradníc q=[q1; q2; q3; q4; q5; q6]T (u robota so šiestimi kĺbmi) a vektor pozície koncového člena robota napríklad efektora P=[x, y, z, α, β, γ]T , tak existuje jednoznačné zobrazenie z priestoru kĺbových súradníc do priestoru kartézskych súradníc, ktoré zapíšeme v tvare P=f(q), čo predstavuje šesť rovníc. Nájdenie týchto rovníc je priama úloha kinematiky. Pohyb robota teda môžeme naprogramovať v priestore kĺbových súradníc a robot vykoná príslušný pohyb v kartézskych súradniciach. Pre človeka je však prirodzenejšie predstaviť si pohyb a plánovať ho v kartézskych súradniciach. U niektorých systémov musíme teda riešiť programovanie obrátenou úlohou a teda zo znalosti pozície P vedieť vypočítať hodnoty kĺbových súradníc. V tomto prípade ide o inverznú úlohu kinematiky, ktorá môže mať viac a dokonca až nekonečno riešení. Pri riešení inverznej úlohy musíme samozrejme uvažovať o pozícii P vo vnútri pracovného priestoru manipulátora. Priemyselné roboty sú programované a následne riadené podľa schémy v nasledujúcom obrázku.

Dráha robota je väčšinou naprogramovaná a uložená vo formáte kĺbových súradníc. Údaje o žiadaných hodnotách kĺbových súradníc qž  sú spolu s príslušným časom uložené v pamäti robota. Riadiaci systém potom pri vykonávaní programu- plánu zaisťuje, že platí q(t) je prakticky rovnaké s qž(t). Priamu úlohu kinematiky pri danom priebehu q(t)tak rieši samotný mechanizmus manipulátora.

Zdroj:

• ŠOLC F., ŽALUD Ľ. 2002. Robotika. s.l. : Fakulta elektrotechniky a komunikačních technologií, Vysoké učení technické v Brně, 2002.